Main research group: Dr G. Zboinski

The main objective of the research in the area of adaptive finite elements is the improvement of existing, and development of new algorithms and programs for the static adaptive analysis of structures. Recently new research has been started on the adaptive modal analysis of complex structures. The main tasks in this particular topic are related to the development of new suitable algorithms and computer programs based on adaptive methods for the finite element method.

Apart from the main implementation problem of hierarchical modelling of complex structures resulting from different degrees of freedom of different theories used for description of various parts of complex structures there are also other implementation problems. They deal with application to complex structures of the most common displacement formulation of the finite element methods, and with employment of the Residual Equilibration Methods (REM) for error estimation. The displacement FEM is sensitive (in the sense that special approach is necessary) to such phenomena as: the improper solution limit of the 3D elasticity model when transverse order of approximation q equals one, shear or shear-membrane locking, and boundary layers typical for thin or thick-walled members of the complex structures. Also REM may suffer from the latter two numerical phenomena. It is also sensitive to edge and corner singularities.

Even though the proposed 3D approach enables usage of the same 3D degrees of freedom within all the complex structure, regardless of the locally applied models, this approach does not remove incompatibility of the first order Reissner-Mindlin model with the hierarchic shell models and with the 3D elasticity. The source of this incompatibility are: the plain stress assumption and kinematic assumption of the theory (no elongation of the normals to the mid-shell surface during deformation). The incompatibility due to the second of the mentioned assumptions can be removed through application of the transition approximations of the displacement field between the first order shell model and hierarchic shell models or three-dimensional elasticity model, while the first one is an inherent feature of the first order shell models and cannot be easily resolved. In our proposition we are not afraid of the latter incompatibility. The method proposed for such situations is controlling the modelling error within the transition zone. This can be done with the same methodology which is used for the first order model itself. Such a control leads to movement of the transition area into the region where this error is acceptable. If such an action is not effective enough then the first order model has to be replaced with the first of the higher order shell models compatible with the description of the remaining part of the complex structure.

Three phenomena - improper solution limit of the 3D elasticity model (with transverse order of approximation q equal to one), locking, and boundary layers need special treatment within displacement FEM formulation (this is also true for some of these phenomena within other FEM formulations). The approach proposed offers local (element level) a posteriori numerical tools for detection and assessment of the mentioned phenomena. This idea is totally original New numerical tools are proposed for detection of the improper solution limit phenomenon, locking phenomena (either shear or shear-membrane), as well as for dectection of boundary layers. The additional advantage is that the proposed tools are compatible with the error estimation procedures that facilitates their implementation. In our proposition two local problems have to be solved for the chosen element of the potentially affected region and the obtained solutions have to compared.

In contrast to a typical case of simple structures a posteriori error estimation within complex structures has to include not only the approximation error but also the modelling error which results from application of mechanical models simplified with respect to 3D elasticity. For the purpose of approximation and modelling error estimation application of the Residual Equilibration Method for all mechanical models included, i.e. 3D-based first order and hierarchic shell models and 3D elasticity model have been proposed. The method is applied twice. First we apply it to approximation error estimation for the elements conforming three mentioned models. For the second time the method is applied for total error estimation within the elements conforming two shell models. The upper bound property of the global total error estimate can be proved for the hierarchic shell models only. Local modelling error indicators are obtained as a difference of the total and approximation indicators.

Some improvement of the estimation in the case of locking, boundary effect and boundary singularities can be gained by constraining local problems or introduction of higher order splitting functions for equilibration instead of linear ones.

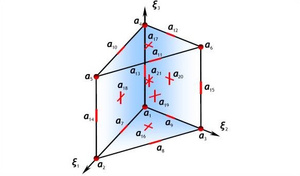
Generalised hierarchical adaptive finite element

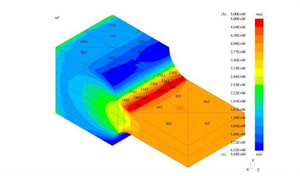
Effective stresses within a complex structure after hp adaptation

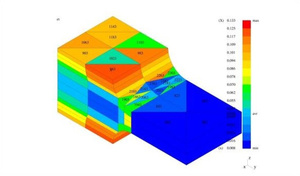
Estimated values of the error within
a complex structure after hp adaptation